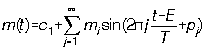Réduction d'une courbe de rotation / de luminosité

Raoul Behrend

Observatoire de Genève

CH-1290 Sauverny

Suisse

raoul.behrend@obs.unige.ch

http://obswww.unige.ch/~behrend

Introduction

Les phénomènes répétitifs et réguliers sont nombreux en astronomie / astrophysique. L'analyse des propriétés de répétition et de ses éventuels variations peut apporter une moisson insoupçonnée de données importantes: rayonnement des astres à la frontière de trous noirs, pulsars, planètes extra solaires, physique des étoiles variables, astéroïdes, détection de satellites gravitant autour d'astéroïdes, etc. Fréquemment, les observations au radar d'astéroïdes demandent d'avoir une courbe de rotation pour être pleinement exploitées. Pareil pour la réduction des occultations par des astéroïdes qui fournissent des formes et dimensions absolues qui, mises en rapport avec l'éclat permettent d'établir de manière très précise l'albébo des diverses familles d'astéroïdes..

De nombreux travaux fort utiles dans la photométrie des étoiles variables ont été réalisés par des amateurs patients et méthodiques. Grâce à l'arrivée des cécédés à prix abordables par des associations voire même des particuliers, des objets présentant des variations de quelques centièmes de magnitude sont désormais accessibles aux amateurs. Malheureusement, les moyens mathématiques et/ou informatiques leurs font parfois défaut pour pouvoir tirer le maximum d'informations de leurs mesures. Cet article a pour objectif d'initier les observateurs au traitement de leurs données. Il est aussi le résumé d'une des conférences du week-end romand des cécédéistes 2001. Il est paru dans la revue Orion 304.

Analyse d'un signal périodique

Pour décrire un phénomène périodique, les mathématiciens utilisent très volontiers les séries dites de Fourier. Sans entrer dans les moindres détails parfois fort subtils, un signal de période est la somme d'un terme constant et de sinusoïdes d'amplitudes et de phases : 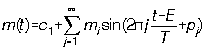. est l'époque, si est le temps, pour laquelle sont spécifiées les phases; les amplitudes ne dépendent pas du choix de l'époque, si on les définit comme étant toujours non négatives, car sinon, la phase serait indéterminée à radians près. En présence d'un signal supposé périodique, l'art de l'analyse consiste à rechercher les valeurs des constantes , , et , après s'être donné . Lorsque est connu ou imposé, la détermination des autres valeurs se nomme calcul de la transformée de Fourier de . Dans certains cas, des outils extrêmement puissants permettent de faire cette opération (transformée de Fourier rapide). Malheureusement, ces méthodes ne peuvent pas être appliquées dans le cas qui nous intéresse ici, car 1) les instants des mesurages ne sont pas toujours régulièrement espacés, 2) la période est inconnue et ne peut pas être divisée a priori régulièrement, 3) les incertitudes ne sont pas les mêmes pour toutes les mesures et 4) la détermination de ne fait pas partie des méthodes habituelles. Question: comment faire ?

Si la période est connue

Supposons dans un premier temps que soit connu ou imposé. En récrivant légèrement différemment la formule de base qui est non linéaire pour la résolution de la phase, on obtient le système entièrement linéaire (=facile à résoudre) suivant: 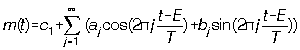. Comme le nombre d'observations n'est pas infini, une limite doit être posée dans la sommation. Cette limite peut être bien plus basse que le nombre d'observations si une méthode de type "moindres carrés" est utilisée. La méthode des moindres carrés à plusieurs inconnues est assez relativement facile à programmer (même dans un tableur) à condition d'utiliser le formalisme des matrices et vecteurs. On écrira par exemple les vecteurs et matrices comme suit: 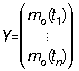qui est la liste des valeurs observées aux instants des mesurages. 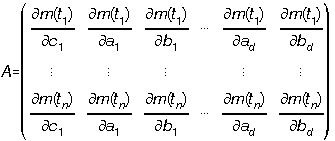est la matrice des dérivées de la fonction à ajuster par rapport à ses paramètres; elle est parfois appelée matrice constitutive. est la matrice carrée de pondération dont les éléments de la diagonale sont et les autres éléments sont nuls; les sont les incertitudes individuelles des mesures. Les inconnues sont 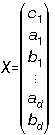. La solution par la méthode des moindres carrés est donnée par . Les symboles et définissent repectivement la transposée et l'inverse de la matrice carrée juste à leurs gauches dans l'expression. Un choix "optimale" de peut se faire comme suit: part de 1 ou 2 et croît jusqu'à ce que les constantes et soient compatibles avec zéro et que les écarts entre valeurs calculées soient compatibles, toujours aux incertitudes près, avec celles observées; un diagramme montrant les couples avec les incertitudes (en tenant compte des covariances !) aide grandement dans ce choix. Habituellement, on se limite à pour les astéroïdes et à pour les binaires à éclipse.

Si la période est inconnue

Dans le cas de inconnu, on procède comme suit. On balaie avec la zone dans laquelle la vraie valeur se cache avec une grande probabilité avec à chaque fois un calcul complet de et des écarts entre observations et valeurs calculées avec les valeurs du obtenu. Les valeurs de pour lesquelles la somme des écarts quadratiques pondérés 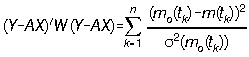est un minimum local sont susceptibles d'être proches de la bonne solution. A ces endroits, on rajoute l'inconnue de la correction à apporter à dans l'expression de la linéarisation: une colonne de plus (constituée des ) dans la matrice et un élément de plus dans le vecteur . Comme cette correction est établie linéairement pour un système non linéaire, quelques cycles de calculs sont à faire avant stabilisation de la solution. Pour avoir une bonne convergence, il faut que l'époque soit proche de la moyenne pondérée des instants des mesurages.

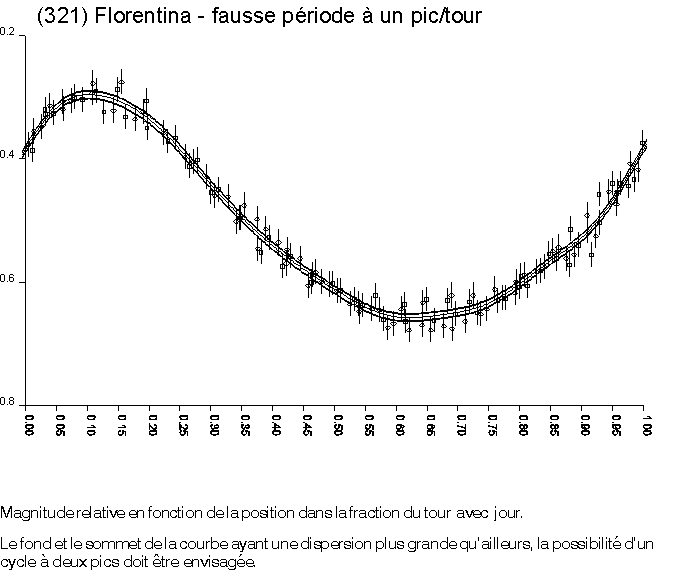
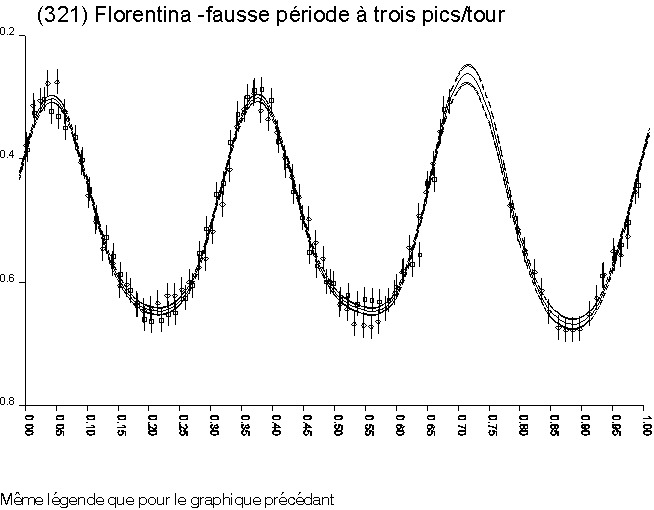
L'expérience montre qu'il faut examiner soigneusement et graphiquement, chaque courbe de rotation/luminosité pour déterminer sa vraisemblance. En effet, des solutions parasites provenant de la fréquence d'échantillonnage trop faible peuvent apparaître; la courbe de luminosité peut également présenter plusieurs pics secondaires d'amplitude similaire (voire même supérieure) au pic principal.

Le cas de (321) Florentina

Mais plutôt que de plus longues formules et développements, prenons un exemple. L'astéroïde (321) Florentina est connu pour avoir une variabilité de quelques dixièmes de magnitude. Olivier Thizy et une équipe du Club d'astronomie Lyon-Ampère (CALA, http://www.cala.asso.fr et http://thizy.free.fr/cala.htm) décidèrent de s'y intéresser lors d'une expédition de photométrie à l'Observatoire du Pic du Château-Renard (AstroQueyras, http://astroqueyras.com). Des images furent prises très régulièrement à l'aide d'une caméra cécédé montée sur un télescope de 620mm d'ouverture et de focale résultante 1.8m durant les nuits du 13 au 15 octobre 1999. Les poses étaient de 120s et le filtre utilisé est en bande R. Une des nuits est décrite comme étant brumeuse dans le rapport de mission ( http://thizy.free.fr/stveran/stveran99.htm ). En l'absence de catalogues photométriques fiables en bande R (erreur systématique possible supérieur à une demi-magnitude), les observateurs ont eu la sagesse de centrer les images de sorte que l'astéroïde puisse être comparé aux mêmes étoiles durant les deux nuits: toutes les mesures sont ainsi en principe cohérentes à quelques centièmes de magnitude. L'échelle de la magnitude est relative à un groupe d'étoile.

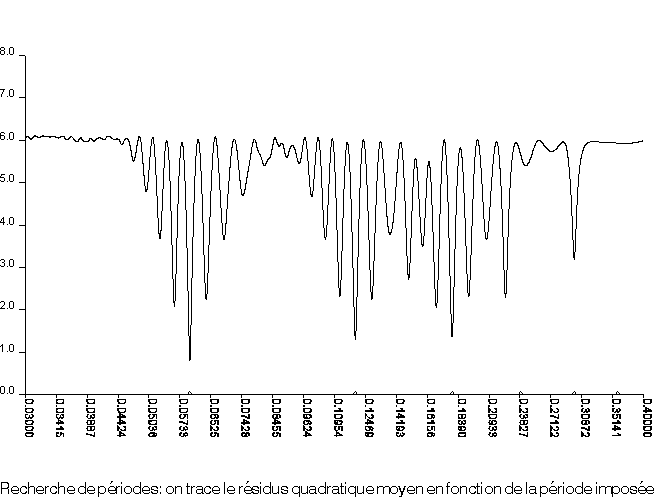
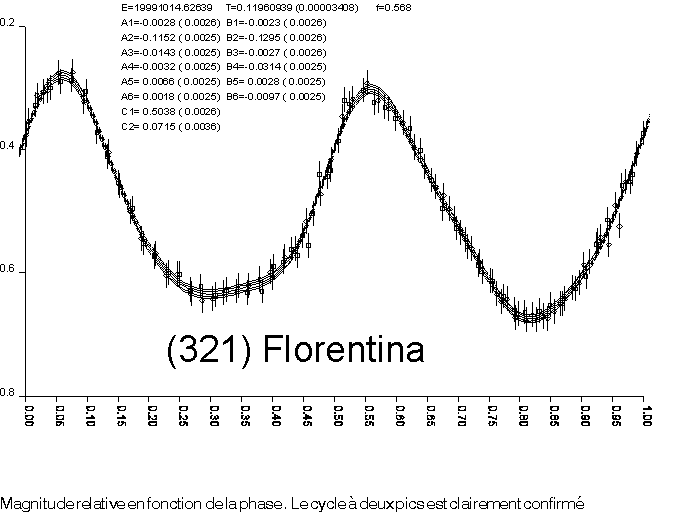
Le graphe de recherche de période indique que jour correspond à une période probable, tout comme ses multiples entiers. Il apparaît également une différence systématique d'éclat entre les deux nuits; cette différence est estimée à magnitude. Elle correspond à l'absorption différente de la lumière par la brume signalée par les observateurs, en fonction de la couleur des étoiles et de l'astéroïde. Pour tenir compte de ce fait, une seconde constante additive est ajoutée au système d'équations pour la seconde nuit; une nouvelle colonne contenant des pour les observations de la première nuit et des pour celles de la seconde est insérée dans la matrice , et l'inconnue est rajoutée dans .

Quelques remarques et conseils

- Il faut veiller à ce que le signal soit théoriquement le plus périodique possible. En particulier, pour les étoiles variables, les périodes et phases n'ont un sens que pour le barycentre du système solaire car elles sont alors indépendantes de la position de la terre. La correction se calcule aisément en coordonnées écliptiques: où est la distance terre-soleil en UA et la longitude écliptique du soleil. et sont les longitude et latitude écliptiques de l'étoile variable. Pour les astéroïdes, les variations intrinsèques de l'éclat par rapport aux changements des distances soleil-astéroïde et astéroïde-terre, et de l'angle soleil-astéroïde-terre sont éliminées en soustrayant la magnitude "moyenne" tirée des éphémérides de la magnitude observée. La période déterminée (apparente) et la phase de l'astéroïde ne sont des valeurs valables que sur un court intervalle de temps; en effet, la période et la phase observées dépendent de la configuration géométrique soleil-astéroïde-terre et de la vitesse angulaire de l'astéroïde (direction et grandeur); en se basant sur plusieurs séries d'observations réparties sur toute l'orbite de l'astéroïde, il est possible de déterminer la période vraie et la direction du pôle de rotation de l'astéroïde; cela peut apporter des contraintes sur sa nature: sablonneux, ou monolithique ?

- Il n'est généralement pas extrêmement utile de faire des mesures sur de nombreuses rotations: une fois la période estimée, il est suffisant de refaire quelques mesures uniquement quand l'incertitude sur la phase atteint environ un dixième de tour. Dans le cas de l'astéroïde présenté, cela correspond à rotations, soit trois mois après la double série initiale.

- Il est extrêmement hasardeux de rechercher une période pour un ensemble de mesures qui ne couvre pas une période complète, avec répétition d'un pic ou d'un creux.

- Il faut inclure dans la formule une constante additive par famille observateur+instrument+filtre+logiciel de réduction, et par zone de catalogue utilisée (dans le cas des GSC, A et SA) ainsi que par nuit problématique (comme dans le cas traité ici). Cette remarque est spécialement valable pour les mesures cécédés faites sans filtre. Si l'albédo de l'astéroïde varie sans que sa couleur ne change, il est théoriquement possible de combiner des observations faites dans des bandes différentes, toujours en rajoutant les inconnues additives ad hoc. Dans le cas des astéroïdes d'amplitude inférieure à magnitude, la multiplication des observateurs ne sert presque à rien s'ils ne font pas plusieurs mesures chacun, car le nombre d'inconnues deviendrait similaire au nombre d'observations, et tous les gains apportés par l'analyse fine (les moindres carrés) s'évaporeraient !

- Pour voir si un astéroïde varie et pour établir une estimation des paramètres de base (, , et ), il n'y a aucune raison de mitrailler à plus que 10 points de mesure par tour ( la période typique est de 0.1-0.2 jours). Un télescope à pointage automatique est capable de suivre à ce rythme une demi-dizaine d'astéroïdes à la fois. Les télescopes automatisés pour la recherche de supernovae peuvent facilement intégrer un astéroïde par nuit dans leurs programmes, avec à chaque fois des résultats de valeur scientifique garantis. L'excès inverse (moins de 1 point par tour) est difficile (mais pas impossible) à exploiter, car il devient difficile de discerner la période vraie des périodes parasites.

- Pour mesurer des variations de quelques centièmes de magnitude, il faut profiter des périodes durant lesquelles l'astéroïde est stationnaire pour avoir toujours les mêmes étoiles de calibration.

- Lorsque le prétraitement des images n'est pas correctement effectué, en particulier si les images des plats (PLU, flats) sont bâclées, une période fictive qui correspond au temps de traversée de l'image par l'astéroïde est créée. Plus les variations que l'on cherche à mesurer sont faibles, et plus grande est l'importance d'un prétraitement complet et correct des images. Une bonne compréhension de la méthode photométrique et l'usage d'un logiciel rigoureux sont également nécessaires pour obtenir des résultats fiables et utilisables.

- Pour les programmeurs mathophobes, , , ,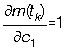

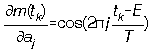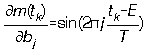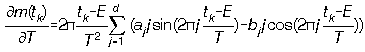
- Il n'est pas nécessaire d'allouer de la mémoire pour entière car seule sa diagonale est non-nulle; il faut alors programmer soi-même les multiplications de matrices

- Un graticiel pour faire les réductions de courbes de rotation/luminosité est disponible sur demande: voir les détails sur http://obswww.unige.ch/~behrend/redcouro/redcouro.html.

Remerciements

Merci à Olivier Thizy et son équipe du Club d'astronomie Lyon-Ampère pour m'avoir permis d'utiliser leurs données pour cet exemple qui combine plusieurs difficultés. Merci également à l'Observatoire du Pic du Château-Renard pour avoir fourni l'instrumentation nécessaire à l'imagerie.

Bibliographie, autres adresses réticulaires

S. Brandt, Statistical and computational methods in data analysis, North-Holland, 1970.

Le site du MAP: http://aude.geoman.fr/observation/map/map.html

Le site du CALL: http://www.minorplanetobserver.com/astlc/default.htm

Le site de Petr Pravec: http://www.asu.cas.cs/~ppravec

Le programme courbrot.exe

Le programme courbrot.exe est conçu pour effectuer les calculs précédents sous dos ou dans une fenêtre dos des pécés. Il prend ses informations dans le fichier courbrot.obs dont le format est décrit ci dessous. La commande de lancement est courbrot numéro . Sans argument, il ne fait que la liste des objets dans la base de données, afin de pouvoir faire le choix du numéro ad hoc. Par exemple:

   1 (321) Florentina

   2 (195) Eurykleia

Pour choisir (321) Florentina, on fait courbrot 1 . Il suffit ensuite de se laisser guider par les choix et valeurs proposées.

Le fichier des observations est dans un format assez strict (pour des raisons historiques, courbrot a près de 12 ans d'âge), c'est-à-dire qu'il faut veiller à aligner correctement les données, en se basant sur un exemple. Les lignes qui commencent par un point-virgule ne sont pas traitées.

;S C Date           T Mes    Sig   Eph

;    aaaammjj.jjjjj   mm.mmm m.mmm mm.mmm

NOM (321) Florentina

PER 0.119

DER 3

DEA 6

EPO 19991015

MES Olivier Thizy

 1 1 19991014.07639 T 00.590

 1 1 19991014.07986 T 00.562

 1 1 19991014.08194 T 00.540

 1 1 19991014.08403 T 00.504

 1 1 19991014.08681 T 00.444

 1 1 19991014.08889 T 00.386

NOM (9117) Aude

PER 0.052

DER 1

DEA 1

H0Z

MES Ch. Demeautis, M. Ory

 1 1  2452041.40932 T 15.95  0.10  15.51

 1 1  2452041.45313 T 16.24  0.10  15.51

 1 1  2452041.46333 T 16.01  0.10  15.51

 1 1  2452041.47737 T 15.98  0.09  15.51

 1 1  2452041.48501 T 15.98  0.10  15.51

 1 1  2452041.50845 T 16.14  0.11  15.51

 1 1  2452041.51921 T 16.11  0.13  15.51

 1 1  2452041.52940 T 16.04  0.11  15.51

 1 1  2452041.54062 T 16.01  0.13  15.51

 1 1  2452041.55006 T 16.05  0.13  15.51

 1 1  2452042.33848 T 16.11  0.19  15.53

 2 1  2452042.35422 T 15.91  0.08  15.53

 2 1  2452042.36829 T 15.99  0.08  15.53

Les dessins et graphes sont en hpgl, le langage universel des tables traçantes. La plupart des texteurs les récupèrent sans trop de difficultés. Si vous n'en disposez pas, hp2xx fera très bien l'affaire !

courbrot est un timbriciel (tout comme les logiciels du site ftp://obsftp.unige.ch/pub/behrend): c'est-à-dire qu'il est gratuit pour toutes les applications non commerciales, mais que l'auteur désire recevoir en échange de son travail de développement une carte postale avec un superbe timbre. Un petit "merci" dans les éventuelles publications serait très apprécié.