Exercice 5 - Introduction to Cosmological N-body Simulations¶
(This exercise is inspired from a hands-on session given by Volker Springel in 2013)
In this practical work, we will simulate the evolution of a portion of a
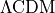 universe, from very high redshift up to the present time.
The work is divided into the following steps:
universe, from very high redshift up to the present time.
The work is divided into the following steps:
As a complement to this page, you can read this presentation (pdf file).
You will need to have a personal directory in the /scratch directory on lesta. Ask the system manager (by emailing astro-it-support@unige.ch) in order to get one. You will also need special privileges to run jobs using sbatch, so ask for this as well at the same time.
5.0 - Setup lesta¶
Make sure you are familiar with the lesta documentation before starting this exercise. (Note: avoid using a conda environment while compiling the C code. Run conda deactivate before loading the modules.)
We will be using openmpi version 1.10.2 due to compatibility reasons with the C codes involved. Load this by typing
$ module add GCC/4.9.3-2.25
$ module add OpenMPI/1.10.2
$ module add FFTW/2.1.5
$ mosule add HDF5/1.8.17
5.1 - Generate the initial conditions¶
Initial conditions for cosmological simulations are based on the power spectrum of visible matter in our large-scale Universe. The latter is derived from direct observations provided by large galaxy surveys, weak lensing surveys, Lyman alpha absorption, and also from the cosmic microwave background.
To generate initial conditions for cosmological simulations, we usually proceed through the following steps :
Setup a Cartesian grid with dimensions corresponding to the volume of the simulated universe. Periodic boundaries will be applied.
Compute the perturbation field using the inverse Fourier transform of the power spectrum.
Compute the perturbation of the velocities following the Zel’dovich approximation.
Apply these perturbations to the Cartesian grid.
Different codes have been developed to generate initial conditions. Here, we will use a parallel code called
N-GenIC developed by Volker Springel.
In order to use this code, you need to :
Download it. You can do this, for example, inside a directory called
TP4that you create in your home directory. To be able to download files from URLs, you need to be connected to one of the login nodes (e.g. login01, login02, etc.) rather than on lesta (which is used to perform the actual computations).$ mkdir TP4 $ cd TP4 $ wget http://www.mpa-garching.mpg.de/gadget/n-genic.tar.gz $ tar -xzf n-genic.tar.gz $ cd N-GenIC/Edit the Makefile by adding the following lines above the first instance of
ifeq ($(SYSTYPE), ...)ifeq ($(SYSTYPE),"lastro_TP4") CC = mpicc OPTIMIZE = -Wall GSL_INCL = GSL_LIBS = FFTW_INCL= -I /opt/ebsofts/MPI/GCC/4.9.3-2.25/OpenMPI/1.10.2/FFTW/3.3.4/include FFTW_LIBS= -L /opt/ebsofts/MPI/GCC/4.9.3-2.25/OpenMPI/1.10.2/FFTW/3.3.4/lib MPICHLIB = endifwhich sets the paths to some required libraries. In order to use these definitions when compiling the code, change the line
SYSTYPE="OPA-Cluster64-Gnu"to
SYSTYPE="lastro_TP4"Note that there will be many “SYSTYPE=…” lines that are commented out (i.e. ignored by the compiler) above the one you change.
Back at the command line, compile the code.
$ makeIf successful, this will create a binary called
N-GenICin the current directory. (Don’t worry if you get a few warnings about unused variables.)
In order to execute N-GenIC, we need to provide it with some parameters. An example
file containing these parameters is given in ics.param. Useful parameters are:
parameter name |
value |
description |
|---|---|---|
|
150000.0 |
Periodic box size of simulation |
|
0.3 |
Total matter density (at z=0) |
|
0.7 |
Cosmological constant (at z=0) |
|
0.7 |
Hubble parameter |
|
0.9 |
Power spectrum normalization |
|
63 |
Starting redshift |
You can leave these as their default values.
HubbleParam corresponds to the commonly used little 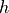 , which is linked to the Hubble constant through:
, which is linked to the Hubble constant through:
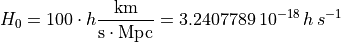
Units are defined by the following parameters
parameter name |
value |
description |
|---|---|---|
|
3.085678e21 |
defines length unit of output (in cm/h) |
|
1.989e43 |
defines mass unit of output (in g/h) |
|
1e5 |
defines velocity unit of output (in cm/s) |
For the sake of simplicity, change the parameter controlling the number of files written in parallel to 1, i.e.
NumFilesWrittenInParallel 1
Other parameters may be kept unchanged. To run the code, simply type
$ mkdir ICs
$ mpirun -n 1 ./N-GenIC ics.param
You should end up with a file called ICs/ics.
5.2 - Run the simulation¶
In the previous part, we have setup initial conditions, where positions, velocities, and masses of
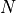 particles have been defined. The second step is to let the system evolve under gravitational forces.
We will hereafter neglect all other types of forces, for example pressure forces. We thus assume that
the system is composed of collisionless dark matter only.
particles have been defined. The second step is to let the system evolve under gravitational forces.
We will hereafter neglect all other types of forces, for example pressure forces. We thus assume that
the system is composed of collisionless dark matter only.
Basically, what we need to do is to integrate 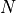 equations of motion, where
equations of motion, where 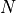 corresponds to the number of particles.
At each time step, the forces acting on each particle depend on the positions of all others. On top of that,
the expansion of the universe must be taken into account. By using a so-called ‘comoving’ reference frame, it is possible
to absorb the expansion of the universe into the equations of motion.
corresponds to the number of particles.
At each time step, the forces acting on each particle depend on the positions of all others. On top of that,
the expansion of the universe must be taken into account. By using a so-called ‘comoving’ reference frame, it is possible
to absorb the expansion of the universe into the equations of motion.
In practice, computing the forces on 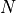 particles due to
particles due to 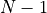 other particles is far from trivial, as the
problem scales as
other particles is far from trivial, as the
problem scales as 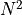 . We will simply use here an open source code called
. We will simply use here an open source code called Gadget-2 designed to solve
this kind of problem.
The full documentation for Gadget-2 may be found here.
In order to use Gadget-2, do the following:
From your working directory (e.g.
~/TP4), download and extract the Gadget-2 source code.$ wget http://www.mpa-garching.mpg.de/gadget/gadget-2.0.7.tar.gz $ tar -xzf gadget-2.0.7.tar.gz $ cd Gadget-2.0.7/Gadget2/Edit the Makefile with the following changes :
increase the size of the mesh needed by the particle mesh (PM) gravity solver
OPT += -DPMGRID=256This will better suit our
particle set-up.
compute the potential energy
OPT += -DCOMPUTE_POTENTIAL_ENERGYwrite the potential and acceleration in the snapshot files
OPT += -DOUTPUTPOTENTIAL OPT += -DOUTPUTACCELERATIONas previously, add a block that defines the path to some needed libraries
ifeq ($(SYSTYPE),"lastro_TP4") CC = mpicc OPTIMIZE = -O3 -Wall GSL_INCL = GSL_LIBS = FFTW_INCL= -I /opt/ebsofts/MPI/GCC/4.9.3-2.25/OpenMPI/1.10.2/FFTW/3.3.4/include FFTW_LIBS= -L /opt/ebsofts/MPI/GCC/4.9.3-2.25/OpenMPI/1.10.2/FFTW/3.3.4/lib MPICHLIB = HDF5INCL = -DH5_USE_16_API HDF5LIB = -lhdf5 -lz endifIn order to use this block, change
SYSTYPE="MPA"to
SYSTYPE="lastro_TP4"Compile.
$ makeThis should compile the code and create a binary called
Gadget2.
Now, prepare the directory where you will run the simulation.
Then, assuming that your user name is
lastro_etu, create a directory that will contain the simulation.$ mkdir /scratch/lastro_etu/lcdm256-001 $ cd /scratch/lastro_etu/lcdm256-001
Copy the sources into this directory that you just compiled.
$ cp ~/TP4/Gadget-2.0.7/Gadget2/ src(This assumes you have downloaded
gadgetinto a folder calledTP4in your home directory. Change the path to suit your setup if necessary.)Similarly copy the initial conditions.
$ cp ~/TP4/N-GenIC/ICs .Create a new directory that will store the output files.
$ mkdir snapCreate a file that will contain the list of time coordinates (as scale factors) of when you want to store snapshots (A snapshot refers to the state of the entire system at a fixed moment in time.). It could look something like this:
0.0625000000 0.1250000000 0.1875000000 0.2500000000 0.3125000000 0.3750000000 0.4375000000 0.5000000000 0.5625000000 0.6250000000 0.6875000000 0.7500000000 0.8125000000 0.8750000000 0.9375000000 1.0000000000Copy an example parameter file.
$ cp ~/TP4/Gadget-2.0.7/Gadget2/parameterfiles/lcdm_gas.param paramsEnable snapshots to be written in hdf5 format:
SnapFormat 3Edit this file to setup specific parameters for your configuration:
InitCondFile path_to_your_ICs OutputDir path_to_your_output_directory %(where the snapshots will be saved) [...] OutputListFilename path_to_your_file_containing_output_times %(created in point 6)Make sure that the internal units are consistent with your previous definition:
UnitLength_in_cm UnitMass_in_g UnitVelocity_in_cm_per_sSet the beginning and end of the simulation to scale factors corresponding to a redshift of 63 and 0 (present day):
TimeBegin give a value here TimeMax give a value hereVerify the cosmological parameters, as well as the size of the box. These must be the same as the ones used in
N-GenIC:Omega0 0.3 OmegaLambda 0.7 OmegaBaryon 0.0 HubbleParam 0.7 BoxSize 150000.0Set a gravitational softening length of order
the mean particle spacing, fixed in comoving coordinates:
SofteningHalo give a value here [...] SofteningHaloMaxPhys give a value here(It might help to recall that our simulation has
particles.)
And finally, run the simulation. As we will run it in parallel using the queue system of lesta
(see the documentation),
you first need to create a batch script, which we’ll call start.slurm. In this file, put
#!/bin/bash
#SBATCH --job-name TP4
#SBATCH --error error.e%j
#SBATCH --output out.o%j
#SBATCH --ntasks 8
#SBATCH --partition p4
#SBATCH --time 0-10:00:00
module purge
module load GCC/4.9.3-2.25
module load OpenMPI/1.10.2
module load FFTW/2.1.5
module load HDF5/1.8.17
mpirun ./Gadget2 path_to_your_parameter_file > gadget2_out.txt
Then, to submit the job, simply type
$ sbatch start.slurm
This will run the simulation on the queue named p4 using 8 cpus for a maximum time of 10 hours.
To check that your simulation is running, type
$ squeue -u your_username
and you should see your job listed.
Using 8 cpus, the simulation should take less than one hour.
The file gadget2_out.txt contains the standard I/O outputs.
You can tail it to follow the progress of the simulation:
$ tail -n 100 gadget2_out.txt
5.3 - Analyse the results¶
Let’s take a look at it¶
It is always interesting to have a look at a simulation, as the human eye is very good at spotting suspicious artefacts. To do that use Python to read in one of the snapshots. Here is an example on how to read in an hdf5 snapshot. The data and header of the file will be saved into Python dictionaries, explore them to familiarise with the fields:
import h5py
f = h5py.File(snapshot_name, 'r')
header = {}
data = {}
for item in f['Header'].attrs:
header[item] = f['Header'].attrs[item]
for item in f['PartType1'].keys():
data[item] = f['PartType1'][item][:]
f.close()
Now use Python to produce a simple plot, either just the positions of the particles (with plt.scatter()), or create
a column density map (hint: use np.histogram2d()).
A movie can then be created by using the Python module animation. Build upon this code snippet:
import matplotlib.animation as animation
fig, ax = plt.subplots(figsize=[10,10], dpi=100)
def plot_stuff(isnap):
#This function will be iterated by the animation.FuncAnimation function with a different snapshot number isnap.
#It should therefore read in snapshot number isnap and produce the plot.
ax.clear()
ax.imshow( np.log10(ColumnDensity), vmin=vmin, vmax=vmax, extent=extent, cmap=cmap )
ani = animation.FuncAnimation(fig, plot_stuff, frames = range(0,finsnap), interval=100)
ani.save('Gadget.gif')
If the simulation was successful, you should see the growth of large scale structures.
At 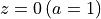 the universe should be similar to the one displayed in Fig. 2.
the universe should be similar to the one displayed in Fig. 2.

Fig.2 : Surface density of a simulated universe at 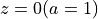 .¶
.¶
Extracting haloes¶
In the previous section, we have seen that from the initially nearly homogeneous universe, structures emerge and grow under the action
of gravity. At 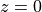 , a large number of clusters (or haloes) seem to be present. In order to characterise
the state of the universe at
, a large number of clusters (or haloes) seem to be present. In order to characterise
the state of the universe at 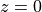 , it is common to compute the so-called “halo mass function”, i.e., the number of haloes
within a given range of mass.
, it is common to compute the so-called “halo mass function”, i.e., the number of haloes
within a given range of mass.
However, to do so, it is first necessary to extract those haloes from the final snapshot. This part is far from trivial and
different algorithms exist for this purpose. In this work, we will use the classical Friends of Friends (FoF) algorithm, implemented here in a code
called FoF_Special kindly provided by Volker Springel.
In short, the idea of a FoF algorithm is the following: each particle belongs to a group of particles made of neighbouring particles (friends) lying within a distance smaller than a given linking length (a fixed parameter). If two particles have one or more common neighbouring particles, the group is merged. At the end of the procedure, a number of groups exist. The algorithm guarantees that within a group, all particles are friends of friends of friends etc. and that no particles outside of this group have friends inside of the group. That is, no particle in the group is situated at a distance smaller than the linking length with respect to any particle outside.
To use FoF_Special first download it and extract it.
Before compiling, we need to setup the linking length. This is hardcoded in the file main.c, and its value
is given in term of mean particle separation. You can leave its default value.
double LinkLength = 0.2;
Then, compile the code by typing
$ make
If you encounter an error related to stddef.h, it means the wrong C compiler is being used.
Edit the Makefile so that the compiler specification line reads
CC = gcc
Try compiling again by running
$ make clean
$ make
You should end up with a binary called FoF_Special.
To apply FoF_Special on the snapshots of our simulation we will proceed as follows:
In the directory where you ran the simulation, create a folder called
fofand copyFoF_Specialthat you just created.Then, run
FoF_Specialon the last snapshot, which should correspond to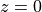 . You need to provide
. You need to provide FoF_Specialwith three arguments: the output directory, the basename of the snapshot files, and the number of the output for which you want to extract haloes. This yields:./FoF_Special . ../snap/snapshot 32
Three directories are created:
groups_catalogue,groups_indexlist,groups_particles. Each contains a file labeled with the snapshot number. Files in the directorygroups_cataloguecontain information on the groups, whilegroups_particlescontains the positions of particles in groups. We will not use the files in the directorygroups_indexlist.
In order to use the output files, we provide students with a small Python library that will help the reading of these files.
The module is given in the FoFlib.py script. Note that you will likely need to modify the lines in the methods
where files are opened to read:
f = open(filename,'rb')
since the files to be read are in binary format.
The mass function of dark haloes¶
One common way to characterise the structure of a universe is to measure the statistical properties of its haloes. The simplest statistic we can perform is to count the number of haloes found for a given mass interval, normalised to the volume of the universe that contains those structures. This function is usually called the “halo mass function”.
The structure of dark haloes¶
According to the 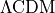 paradigm, galaxies form inside dark haloes.
Studying the structures of those haloes allows us to make a direct link between the predictions
of numerical simulations and observations. Thus, once haloes have been extracted, it is interesting
to compute properties like their density profiles or rotation curves.
paradigm, galaxies form inside dark haloes.
Studying the structures of those haloes allows us to make a direct link between the predictions
of numerical simulations and observations. Thus, once haloes have been extracted, it is interesting
to compute properties like their density profiles or rotation curves.
