A natural scale of stellar masses
Chandrasekhar argued that for a star to be mechanically stable, the following inequality has to be satisfied (the density is supposed to decrease outwards):
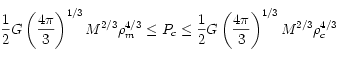
Here, ρm is the mean density and ρc the central density. Pc is the sum of gas pressure plus radiation pressure at the centre. The right hand side of the inequality gives the necessary condition for the stability of a star, i.e. ![\mu^2M\left(\frac{\beta_c^4}{1-\beta_c}\right)^{1/2}\geq 0.19\left[\left(\frac{hc}{G}\right)^{3/2}\frac{1}{m_p^2}\right]](local/cache-vignettes/L263xH61/dea5b015410067a9891aac18eebb848c-d4b64.png "\mu^2M\left(\frac{\beta_c^4}{1-\beta_c}\right)^{1/2}\geq 0.19\left[\left(\frac{hc}{G}\right)^{3/2}\frac{1}{m_p^2}\right]")
The combination of fundamental constants on the right hand side has the dimension of MASS. Its value is 29.2 solar masses. We thus see that in a theory of stars where gravity is balanced by the sum of gas pressure and radiation pressure, the natural scale of mass is of stellar magnitude. This is why the stars are as they are ! Or, as Chandrasekhar put it:
"We conclude that to the extent the above theory is at the base of the equilibrium of actual stars, to that extent the above combination of natural constants, providing a mass of proper magnitude for the measurement of stellar masses, is at the base of a physical theory of stellar structure.’’
Taken from G. Srinivasan (1995) in Saas-Fee Advanced Course 25, p.101
The following table displays central densities, temperatures, gaz and radiative pressure as well as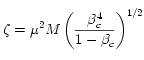 
on the ZAMS for various initial mass models (assuming μ=0.615). The values are taken from Geneva stellar models.
| Mass | ρc | Tc | Pgas | Prad | βc | ζ |
|---|---|---|---|---|---|---|
| [Mo] | [g/cm3] | [106 K] | [1016 g/(cm s2)] | [1016 g/(cm s2)] | [Mo] | |
| 1 | 78.5 | 13.2 | 13.89 | 0.01 | 0.9993 | 14.3 |
| 3 | 40.8 | 24.0 | 13.12 | 0.08 | 0.9940 | 14.5 |
| 9 | 10.5 | 31.0 | 4.36 | 0.23 | 0.9499 | 13.7 |
| 20 | 4.9 | 36.1 | 2.37 | 0.43 | 0.8464 | 13.8 |
| 60 | 2.3 | 41.3 | 1.27 | 0.73 | 0.6350 | 15.2 |