Chemistry C API¶

Some Definitions¶

The mass of element i ejected by a SNII and synthesized by a star of mass m writes:

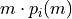
$m\cdot p_i(m)$

The mass of element i ejected by a SNII issue from the non processed part of a star of mass m writes:

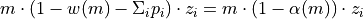
$m\cdot \left( 1 - w(m) - \Sigma_i p_i\right) \cdot z_i = m\cdot \left( 1 - \alpha(m) \right) \cdot z_i$

Where we have defined the helium core mass fraction 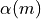$\alpha(m)$ as:

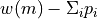
$w(m) - \Sigma_i p_i$

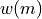with $w(m)$ , the mass of the remnant.

Some variables¶

Elt¶: table containing 1-helium core, 1-residual and yields for all elements

$\texttt{Elt[0].Array[j]} = \int_{0}^{m_j} \left(1-\omega(m)\right) \Phi(m)\,dm \texttt{Elt[1].Array[j]} = \int_{0}^{m_j} \left(1-\alpha(m)\right) \Phi(m)\,dm \texttt{Elt[i+2].Array[j]} = \int_{0}^{m_j} p_i(m) \Phi(m)\,dm$

$\texttt{Elt[0].Metal[j]} = 1-\omega(m_j) \texttt{Elt[1].Metal[j]} = 1-\alpha(m_j) \texttt{Elt[i+1].Metal[j]} = p_i(m_j)$

$\texttt{Elt[i+1].MSNIa} = \textrm{mass of element i ejected by a WD} = m_{WD}\,p_i$

$\texttt{Cps[it].Mco} = \textrm{white dwarf mass} = m_{\rm{WD}}$

Initialisation functions¶

void allocate_chimie()¶: This function allocates all varaiables related to the chemistry

void set_table(int i)¶: Set the chemistry table to use

void read_chimie(char * filename, int it)¶: Read the chemistry table

void init_chimie(void)¶: This function initializes the chemistry parameters

void check_chimie(void)¶: This function performe simple checks to validate the chemistry initialization

int get_nelts()¶: Return the number of elements considered

float get_SolarMassAbundance(i)¶: Return the solar mass abundance of elt i

char* get_Element(i)¶: Return the label of element i

IMF functions¶

static double get_imf(double m)¶: This function returns the mass fraction of a star of mass m using the current IMF

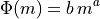
$\Phi(m) = b\, m^a$

static double get_imf_M(double m1, double m2)¶: This function returns the mass fraction between m1 and m2 per mass unit, using the current IMF

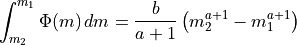
$\int^{m_1}_{m_2} \Phi(m)\,dm = \frac{b}{a+1} \left( m_2^{a+1} - m_1^{a+1} \right)$

static double get_imf_N(double m1, double m2)¶: This function returns the number fraction between m1 and m2 per mass unit, using the current IMF

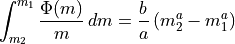
$\int^{m_1}_{m_2} \frac{\Phi(m)}{m}\,dm = \frac{b}{a} \left( m_2^{a} - m_1^{a} \right)$

static double imf_sampling()¶: Sample the imf using monte carlo approach

void init_imf(void)¶: This function initializes the imf parameters defined in the chemistry file. It compute the normalization factor 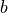$b$ ensuring: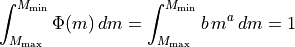

$\int^{M_{\rm{min}}}_{M_{\rm{max}}} \Phi(m)\,dm = \int^{M_{\rm{min}}}_{M_{\rm{max}}} b\, m^a \,dm = 1$

Lifetime functions¶

double star_lifetime(double z, double m)¶: Return the lifetime of a star of mass m and metallicity z

double star_mass_from_age(double z, double t)¶: Return the mass of a star having a livetime t and a metallicity z

Dying stars functions¶

number of dying stars in a mass range¶

double DYIN_rate(double m1, double m2)¶: compute the number of stars between m1 and m2 masses in code unit

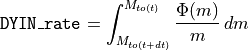
$\texttt{DYIN\_rate} = \int^{M_{to(t)}}_{M_{to(t+dt)}} \frac{\Phi(m)}{m}\,dm$

double SNII_rate(double m1, double m2)¶: compute the number of SNII between m1 and m2 masses in code unit

double SNIa_rate(double m1, double m2)¶: compute the number of SNIa between m1 and m2 masses in code unit

DYIN mass ejection¶

void DYIN_mass_ejection(double m1, double m2)¶

Compute the mass fraction and yields of dying stars with masses between m1 and m2. Only masses lower than 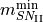$m_{SN_{\rm{II}}}^{\rm{min}}$ are conserned. Store the result in the global variable MassFracDYIN:

MassFracDYIN[0] = total gas
MassFracDYIN[1] = helium core  (i.e. alpha(m))
MassFracDYIN[i] = frac mass elt i.

$\texttt{MassFracDYIN[0]} = \int^{M_{to(t)}}_{M_{to(t+dt)}} \left(1-\omega(m)\right) \Phi(m)\,dm \texttt{MassFracDYIN[1]} = \int^{M_{to(t)}}_{M_{to(t+dt)}} \left(1-\alpha(m)\right) \Phi(m)\,dm \texttt{MassFracDYIN[i+2]} = \int^{M_{to(t)}}_{M_{to(t+dt)}} p_i(m) \Phi(m)\,dm$

void DYIN_single_mass_ejection(double m1)¶

Compute the mass fraction and yields of a dying stars of masse m1. Only masses lower than 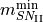$m_{SN_{\rm{II}}}^{\rm{min}}$ are conserned. Store the result in the global variable SingleMassFracDYIN:

SingleMassFracDYIN[0] = total gas
SingleMassFracDYIN[1] = helium core  (i.e. alpha(m))
SingleMassFracDYIN[i] = frac mass elt i.

$\texttt{MassFracDYIN[0]} = 1-\omega(m1) \texttt{MassFracDYIN[1]} = 1-\alpha(m) \texttt{MassFracDYIN[i+2]} = p_i(m)$

SNII mass ejection¶

void SNII_mass_ejection(double m1, double m2)¶

Warning

in the old version the mass ejected by SNII also included the mass ejected by smaller mass objects. This is now corrected.

Compute the mass fraction and yields of SNII stars with masses between m1 and m2. Only masses in the range $[m_{SN_{\rm{II}}}^{\rm{min}},m_{SN_{\rm{II}}}^{\rm{max}}]$ are conserned. Store the result in the global variable MassFracSNII:

MassFracSNII[0]   = total gas per mass unit = 1-w      (1 - mass fract of residual)
MassFracSNII[1]   = 1-helium core                      (i.e. non processed elts)
MassFracSNII[i+2] = mass fract of elt i.               (syntetised elts)

$\texttt{MassFracSNII[0]} = \int^{M_{to(t)}}_{M_{to(t+dt)}} \left(1-\omega(m)\right) \Phi(m)\,dm \texttt{MassFracSNII[1]} = \int^{M_{to(t)}}_{M_{to(t+dt)}} \left(1-\alpha(m)\right) \Phi(m)\,dm \texttt{MassFracSNII[i+2]} = \int^{M_{to(t)}}_{M_{to(t+dt)}} p_i(m) \Phi(m)\,dm$

void SNII_single_mass_ejection(double m1)¶

Warning

in the old version the mass ejected by SNII also included the mass ejected by smaller mass objects. This is now corrected.

Compute the mass fraction and yields of a SNII stars of masse m1. Only masses in the range $[m_{SN_{\rm{II}}}^{\rm{min}},m_{SN_{\rm{II}}}^{\rm{max}}]$ are conserned. Store the result in the global variable SingleMassFracSNII:

SingleMassFracSNII[0]   = total gas per mass unit = 1-w      (1 - mass fract of residual)
SingleMassFracSNII[1]   = 1-helium core                      (i.e. non processed elts)
SingleMassFracSNII[i+2] = mass fract of elt i.               (syntetised elts)

$\texttt{MassFracSNII[0]} = 1-\omega(m1) \texttt{MassFracSNII[1]} = 1-\alpha(m) \texttt{MassFracSNII[i+2]} = p_i(m)$

SNIa mass ejection¶

void SNIa_mass_ejection(double m1, double m2)¶

Compute the total mass and element mass per mass unit of SNIa stars with masses between m1 and m2. Store the result in the global variable MassFracSNIa:

MassFracSNIa[0]   = total gas per mass unit = 1-w      (1 - mass fract of residual)
MassFracSNIa[1]   = -1                                 (unused)
MassFracSNIa[i+2] = mass fract of elt i.               (SNIa yields)

$\texttt{MassFracSNIa[0]} = N_{Ia}^{\rm{spec}}\,m_{WD} \texttt{MassFracSNIa[i+2]} = N_{Ia}^{\rm{spec}}\,m_{WD}\,p_i$

void SNIa_single_mass_ejection(double m1)¶

Compute the total mass mass of element of a SNIa stars of masse m1. Store the result in the global variable SingleMassFracSNIa:

SingleMassFracSNIa[0] = total gas per mass unit = 1-w      (1 - mass fract of residual)
SingleMassFracSNIa[1] = -1                                 (unused)
SingleMassFracSNIa[i] = mass fract of elt i.               (SNIa yields)

$\texttt{MassFracSNIa[0]} = m_{WD} \texttt{MassFracSNIa[i+2]} = m_{WD}\,p_i$

Total mass ejection¶

void Total_mass_ejection(double m1, double m2, double M0, double *z)¶

Sum the contribution in mass and yields of all stars in the mass range m1,m2. Store the result in the global variable EjectedMass:
EjectedMass[0]   = total gas
EjectedMass[1]   = unused
EjectedMass[i+2] = mass of elt i.
FOR THE MOMENT:
- contrib of SNII (= all stars)
- contrib of SNIa
$\texttt{EjectedMass[0]} = M_0 \left( \int^{M_{to(t)}}_{M_{to(t+dt)}} \left(1-\omega(m)\right) \Phi(m)\,dm + N_{Ia}^{\rm{spec}}\,m_{WD} \right) \texttt{EjectedMass[i]} = M_0 \left( z_i \int^{M_{to(t)}}_{M_{to(t+dt)}} \left(1-\alpha(m)\right) \Phi(m)\,dm + \int^{M_{to(t)}}_{M_{to(t+dt)}} p_i(m) \Phi(m)\,dm + N_{Ia}^{\rm{spec}}\,m_{WD}\,p_i \right)$

Warning

in fact, we do not relly compute 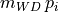$m_{WD}\,p_i$ . This value is already sorted in Elt[i].MSNIa.

void DYIN_Total_single_mass_ejection(double m1, double *z)¶

Mass and element ejected by a single dying stars of mass m1. This takes into account processed and non processed gas The results are stored in:

SingleEjectedMass[0]   = gas mass
SingleEjectedMass[1]   = unsued
SingleEjectedMass[i+2] = mass of elt i.

void SNII_Total_single_mass_ejection(double m1, double *z)¶

Mass and element ejected by a single SNII of mass m1. This takes into account processed and non processed gas The results are stored in:

SingleEjectedMass[0]   = gas mass
SingleEjectedMass[1]   = unsued
SingleEjectedMass[i+2] = mass of elt i.

void SNIa_Total_single_mass_ejection(double m1, double *z)¶

Mass and element ejected by a single SNIa of mass m1. The results are stored in:

SingleEjectedMass[0]   = gas mass
SingleEjectedMass[1]   = unsued
SingleEjectedMass[i+2] = mass of elt i.

void Total_single_mass_ejection(double m1, double *z, double NSNII, double NSNIa, double NDYIN)¶

Sum the contribution in mass and yields of one star of mass m1. Store the result in the global variable EjectedMass:
SingleEjectedMass[0]   = total gas
SingleEjectedMass[1]   = unused
SingleEjectedMass[i+2] = mass of elt i.
FOR THE MOMENT:
- contrib of SNII (= all stars)
- contrib of SNIa
$\texttt{EjectedMass[0]} = m\,[1-\omega(m)] \,N_{DYIN}^{\rm{spec}} + m\,[1-\omega(m)] \,N_{II}^{\rm{spec}} + m_{WD}\,N_{Ia} \texttt{EjectedMass[i+2]} = m \left[ z_i \left(1-\alpha(m)\right) + p_i(m) \right] \,N_{DYIN}^{\rm{spec}} + m \left[ z_i \left(1-\alpha(m)\right] + p_i(m) \right) \,N_{II}^{\rm{spec}} + m_{WD}\,p_i\,N_{Ia}$

Warning

in fact, we do not relly compute 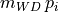$m_{WD}\,p_i$ . This value is already sorted in Elt[i].MSNIa.

Chemistry C API¶

Some Definitions¶

Some variables¶

Initialisation functions¶

IMF functions¶

Lifetime functions¶

Dying stars functions¶

number of dying stars in a mass range¶

DYIN mass ejection¶

SNII mass ejection¶

SNIa mass ejection¶

Total mass ejection¶

Table of Contents

Previous topic

Next topic

This Page