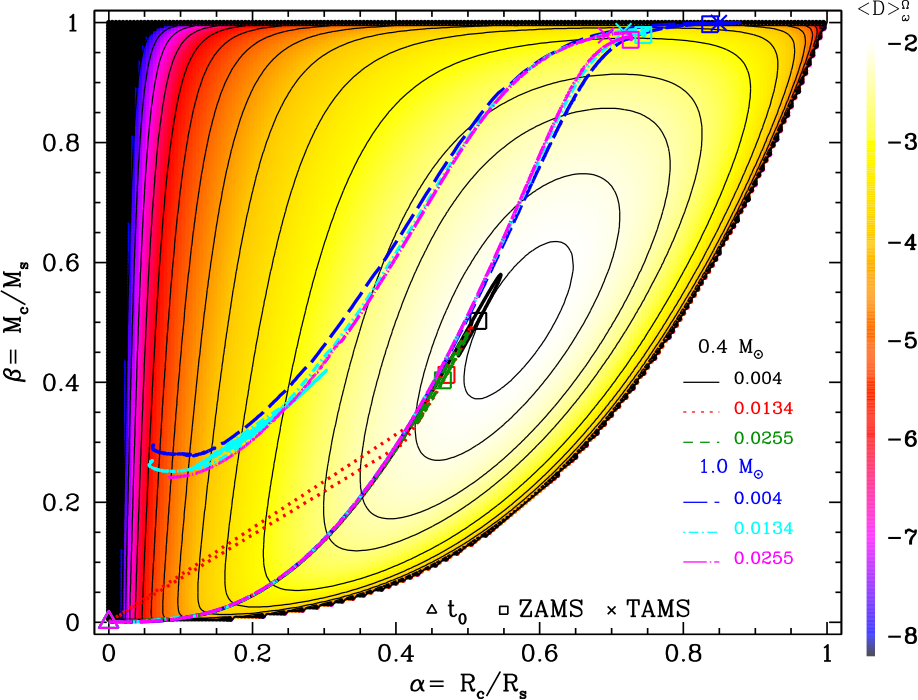
Tidal HRD from Bolmont et al. (2017)
Tidal dissipation in rotating low-mass stars
and implications for the orbital evolution of close-in planets
II. Effect of stellar metallicity
E. Bolmont, F. Gallet, S. Mathis, C. Charbonnel, L. Amard, and Y. Alibert
Abstract
Observations of hot Jupiter type exoplanets suggest that their orbital period distribution depends on the metallicity of their host star. We investigate here whether the impact of the stellar metallicity on the evolution of the tidal dissipation inside the convective envelope of rotating stars and its resulting effect on the planetary migration might be a possible explanation for this observed statistical trend. We use a frequency-averaged tidal dissipation formalism coupled to an orbital evolution code and to rotating stellar evolution models in order to estimate the effect of a change of stellar metallicity on the evolution of close-in planets. We consider here two different stellar masses: 0.4 and 1.0 M⊙ evolving from the early pre-main sequence phase up to the red giant branch. We show that the metallicity of a star has a strong effect on the stellar parameters which in turn strongly influence the tidal dissipation in the convective region. While on the pre-main sequence the dissipation of a metal poor Sun-like star is higher than the dissipation of a metal rich Sun-like star, on the main sequence it is the opposite. However, for the 0.4 M⊙ star, the dependence of the dissipation with metallicity is much less visible. Using an orbital evolution model, we show that changing the metallicity leads to different orbital evolutions (e.g., planets migrate farther out from an initially fast rotating metal rich star). By using this model, we qualitatively reproduced the observational trends of the population of hot Jupiters with the metallicity of their host stars. However, more steps are needed to try to quantitatively fit our results to the observations.
ReadMe.dat
Column 1: Logarithm of the time in yr
Column 2: Stellar luminosity (L☉)
Column 3: Stellar effective temperature (K)
Column 4: Stellar radius (R☉)
Column 5: β = Mass aspect ratio = Mcore/M★
Column 6: α = Radius aspect ratio = Rcore/R★
Column 7: Surface rotation rate of the star (days). Initial rotation = 1.4 days (5.20e-05 s-1)
Column 8: Logarithm of the frequency averaged tidal dissipation (see Eq. 1 of paper I)
Column 9: Logarithm of the modified equivalent quality factor (see Eq. 5 of paper I)
Column 10: Logarithm of the structural frequency-averaged tidal dissipation (see Eq. 3 of paper I)
Column 11: Logarithm of the structural modified equivalent quality factor (see Eq. 6 of paper I)
0.4 M⊙
Z=0.004: M_04_Z_004.csv
Z=0.0134: M_04_Z_0134.csv
Z=0.0255: M_04_Z_0255.csv
1.0 M⊙
Z=0.004: M_10_Z_004.csv
Z=0.0134: M_10_Z_0134.csv
Z=0.0255: M_10_Z_0255.csv
Donwload all: AllDissip.tar.gz
These are condensed grids for which we selected 500 points at most to allow a good description of the full raw tracks. The discription of these 500 points can be found in Lagarde, N., Decressin, T., Charbonnel, C., et al. 2012, A&A, 543, A108 (PDF)
The full grids can be retrieved by sending a request.
Last update: January 18 2019
